[AI] 선형 회귀 (Linear Regression)

이론 빠삭빠삭

선형 회귀 : 가장 훌륭한 예측선 긋기

x변수에 따라서 y값은 변한다.

• x변수가 하나라면 단순 선형 회귀
• x1,x2,x3 … 처럼 변수가 여러개라면 다중 선형 회귀

선형 회귀는 정확한 직선을 그려내는 과정이다.

→ 선형 회귀는 최적의 기울기 a와 y절편 b를 구하는 과정이다.

최소 제곱법 (method of least squares)

변수가 하나 뿐(단순 선형 회귀)이라면 최소 제곱법 (method of least squares)이 사용된다.

오차가 가장적은, 주어진 좌표의 특성을 가장 잘 나타내는 직선을 만들 수 있다.

최소 제곱법에서 기울기 구하기

최소 제곱법에서 y 절편 구하기

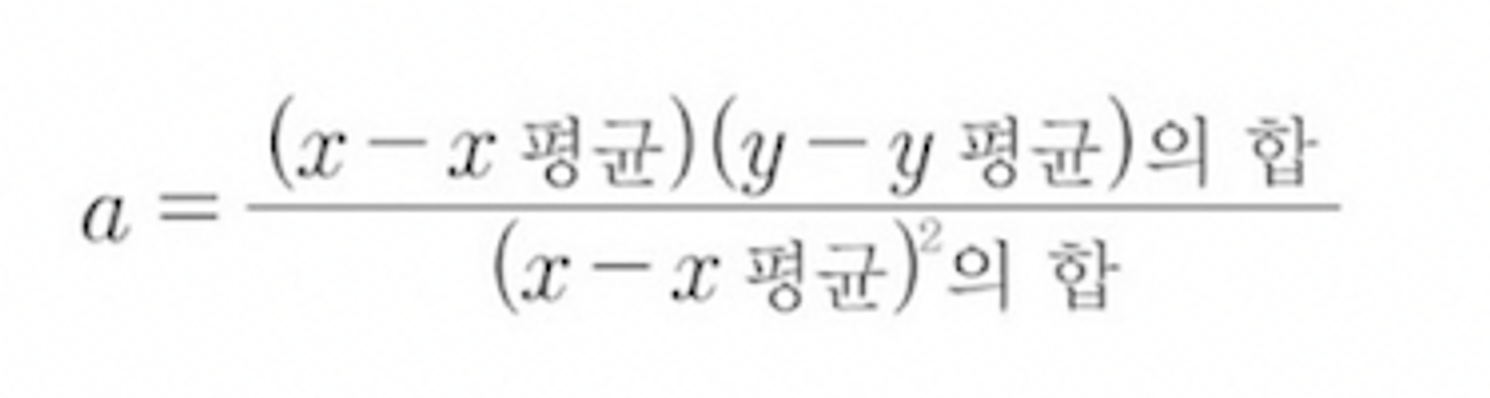
오차 평가 알고리즘

변수가 하나가 아니라 여러 개일 때는 최소 제곱법이 힘들다. 그러니까 임의의 선을 그리고 난 후, 수정하면서 최적의 선을 만들어보자.

→ 일단 그리고 수정한다면 나중에 그린 선이 더 좋은지 안좋은지 판단할 지표가 필요했다.

→ 오차의 합이 최소가 된다면 어떨까? 오차가 음수가 나올 수도 있으니 오차의 제곱의 합이 최소가 된다면?

평균 제곱근 오차 (RMSE, root mean square error)

오차의 제곱의 합을 구해보니 너무 숫자가 크다!

→ 평균을 내보자! → 그래도 숫자가 크다! → 값에 루트를 씌우자!

⇒ 다중 선형 회귀는 평균제곱근오차(RMSE) 값을 가장 작게 만들어주는 작업

⁉️ 오차라는 지표는 알겠는데, 어떤 방식으로 오차를 줄일 것인가 ⁉️

경사 하강법 (gradient descent)

오차를 수정해보자

기울기 값(a)과 오차의 관계

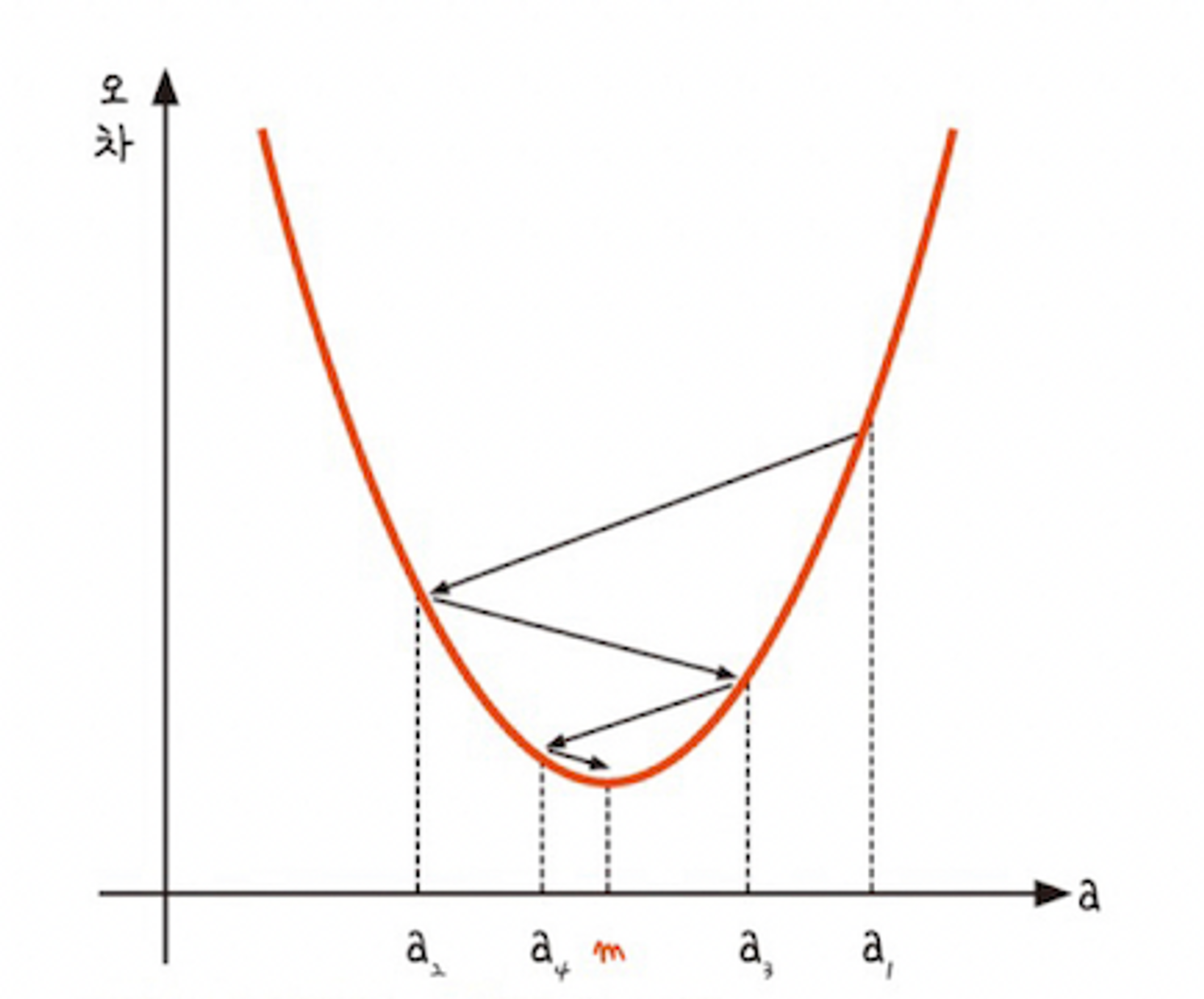
→ 기울기 값이 커지면 오차는 어어엄청 커지고 기울기 값이 작아지면 오차는 다시 어어어어엄청 커진다.

⇒ 기울기가 0인 지점으로 간다면 오차는 가장 작다!

 

✅ 변수가 하나라면 최적의 기울기를 갖는 예측직선이 나오겠지만, 2개라면 예측 평면이 나온다.

 

학습률

기울기를 어느 지점까지 이동시킬지가 중요하다. 이동거리를 정해주는 것이 학습률이다.

(케라스는 학습률을 자동으로 조절해준다고 한다.)

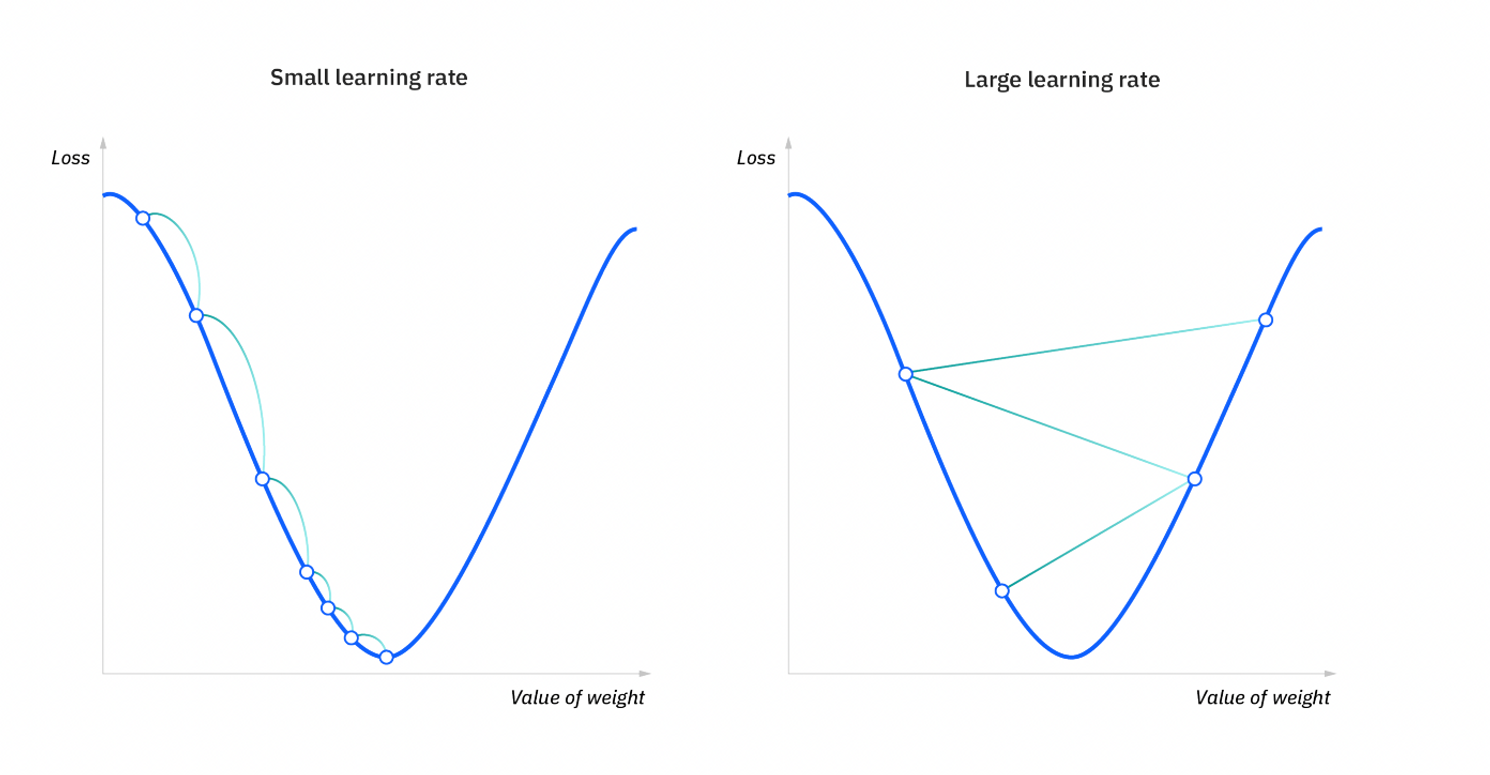
학습률이 너무 작다면 연산이 오래걸리고, 너무 높으면 이상한 곳으로 튕겨져 나갈 수 있다.